Macroscopic quantum self-trapping and Josephson oscillations of exciton polaritons. M. Abbarchi, A. Amo, V. G. Sala, D. D. Solnyshkov, H. Flayac, L. Ferrier, I. Sagnes, E. Galopin, A. Lemaître, G. Malpuech and J. Bloch in Nature Phys. 9:275 (2013). What the paper says!?

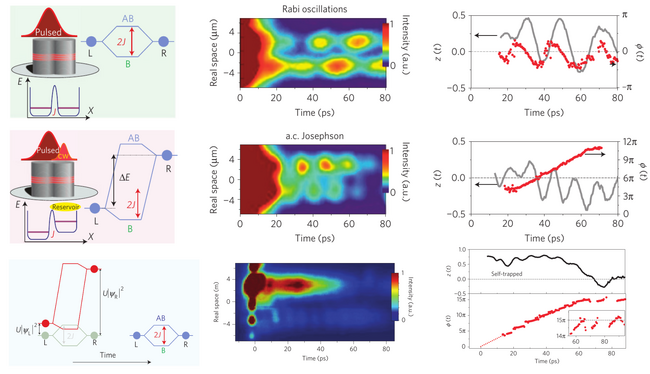
The Authors bring polaritonic Josephson junctions into the nonlinear regime, extending a previous report in the Rabi (linear) regime.[1]
Nonlinear Josephson physics [...] has remained inaccessible in photonic systems because it requires large photon–photon interactions. Here we report on the observation of nonlinear Josephson oscillations of two coupled polariton condensates confined in a photonic
molecule
At low densities they observe the Rabi oscillations, at higher densities, the AC Josephson effect and still higher densities, the macroscopic self-trapping of polaritons in one pillar.
Their equations:
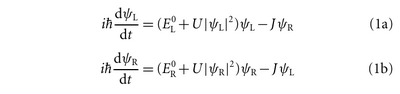
and in their canonical Josephson-dynamics form (population & phase differences):
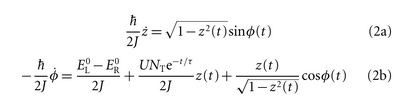
They rightly point out that interactions $U$ are the only term affected by the finite lifetime.
They attribute Josephson regime to a running phase:
A different regime, characterized by a running phase, ...
however, we showed this is not true.[2]
There is a nice overview of the main physics:
Josephson physics shows the most spectacular phenomena in the nonlinear regime, when the interaction energy ($U\vert\psi\vert^2$) is greater than the coupling J. The transfer of particles from one site to the other gives rise to a dynamical renormalization of the energy in each site, resulting in anharmonic oscillations. If interactions are strong enough ($U\vert\psi\vert^2\gg1$), the self-induced energy renormalization quenches the tunnelling, and most of the particles remain localized in one of the sites. This out of equilibrium metastable regime is
called macroscopic quantum self-trapping.